Perbandingan

p 

1. Arti Perbandingan

Perbandingan merupakan suatu hal yang sangat penting dalam matematika, demikian juga dalam kehidupan sehari-hari kita pun tidak lepas dari perbandingan.
Sebagai ilustrasi perhatikan contoh berikut :
a. Usia Ayah 45 tahun dan usia ibu 40 tahun, sedangkan usia Ali 15 tahun serta usia Ani 10 tahun.

Perbandingan usia ayah dan ibu = 45 tahun : 40 tahun = 45 : 40 = 9 : 8
Perbandingan Usia Ali dan Ani = 15 tahun : 10 tahun = 15 : 10 = 3 : 2
Perbandingan usia Ayah dan Ali = 45 tahun : 15 tahun = 45 : 15 = 3 : 1

b. Tinggi badan Dewa 160 cm, tinggi badan Dewi, 120 cm dan tinggi badan Gita 60 cm

Perbandingan tinggi badan Dewa dan Dewi = 160 cm:120 cm = 160:120 = 4:3
Perbandingan tinggi badan Dewi dan Gita = 120 cm:60 cm = 120:60 = 2:1
Perbandingan tinggi badan Dewa dan Gita = 160 cm:60 cm = 160:60 = 8:3

Dari contoh tersebut dapat diketahui bahwa untuk membandingkan dua buah besaran perlu diperhatikan :

a. Bandingkan besaran yang satu dengan yang lain
b. Samakan satuannya
c. Sederhanakan bentuk perbandingannya

Dari uraian dan contoh masalah di atas dapat diperoleh arti perbandingan sebagai berikut :

a. Perbandingan antara a dan b ditulis dalam bentuk sederhanaa a/b  atau a : b, dengan a dan b merupakan bilangan asli, dan b 

 0.

b. Kedua satuan yang dibandingkan harus sama.

c. Perbandingan dalam bentuk sederhana atinya antara a dan b sudah tidak mempunyai faktor persekutuan, kecuali 1.

2. Skala

Istilah skala sering kita jumpai kalau kita membuka peta/atlas.
Jika pada peta tertulis skala 1 : 5.000.000, berarti :
1 cm pada peta mewakili 5.000.000 cm jarak yang sebenarnya, atau
1 cm pada peta mewakili 50.000 m jarak yang sebenarnya, atau
1 cm pada peta mewakili 50 km jarak yang sebenarnya
Skala adalah perbandingan ukuran pada gambar (cm) dengan ukuran sebenarnya (cm) Tampak bahwa skala menggunakan satuan cm untuk dua besaran yang dibandingkan Perlu diingat bahwa : 1 km = 1.000 m = 100.000 cm.
Contoh berikut menjelaskan bagaimana kita menggunakan skala pada sebuah peta.

a. Pada sebuah peta jarak tempat A dan B adalah 3 cm, padahal jarak A dan B sebenarnya 450 km.
Tentukan skala yang dipergunakan pada peta tersebut !

Jawab :
Skala = Ukuran pada peta : Ukuran yang sebenarnya
= 3 cm : 450 km
= 3 cm : 45.000.000 cm (pada skala harus menggunakan satuan cm)
= 3 : 45.000.000
= 1 : 15.000.000

b. Pada sebuah peta jarak kota A ke kota B adalah 8 cm. Jika skala peta itu adalah 1 : 500.000, maka berapakah jarak sebenarnya kedua kota tersebut ?

Jawab :
Skala 1 = 500.000 berarti 1 cm pada peta mewakili jarak 500.000 cm jarak sesungguhnya, atau 1 cm pada peta mewakili jarak 5 km jarak sesungguhnya.

c. Sebuah peta menggunakan skala 1 : 25.000.000 . Jika jarak dua tempat sebenarnya 300 km, berapakah jarak kedua tempat itu pada peta ?

Jawab :
Skala 1 : 25.000.000
Artinya 1 cm pada peta mewakili 25.000.000 cm jarak sesungguhnya, atau 1 cm pada peta mewakili 250 km jarak sesungguhnya.
Jadi jarak kedua tempat itu pada peta adalah 300 : 250 = 1,2 cm

Nah kalian sudah mempelajari perbandingan, skala dan penggunaannya, mudah bukan ?

3.   Skala Sebagai Suatu Perbandingan

Sekarang coba bandingkan ketiga ukuran pas disamping !

Apakah pas foto 2 cm x 3 cm sebanding dengan pas foto 3 cm x 4 cm ?

, ternyata pernyatannya salah, jadi tidak sebanding

Sekarang bandingkan pas foto 2 cm x 3 cm dengan pas foto 4 cm x 6 cm !

, ternyata pernyatannya benar, jadi sebanding

4. Perbandingan Senilai

Perbandingan senilai berkaitan dengan perbandingan dua buah besaran, di mana jika besaran yang satu berubah naik/turun, maka besaran yang lain juga berunah naik/turun.
Contoh masalah yang berkaitan dengan perbandingan senilai adalah :

§  Jumlah barang yang dibeli dengan harga yang harus di bayar

§  Jumlah konsumsi bahan bakar dan jarak yang ditempuh

§  Jumlah kaleng cat dan luas permukaan yang bisa di cat

§  dan lain-lain

Cara menyelesaikan masalah perbandingan senilai adalah dengan :
a. Menentukan nilai satuan
Dilakukan dengan menentukan nilai satuan dari besaran yang dibandingkan, baru kemudian dikalikan dengan besaran yang ditanyakan.
b. Menuliskan perbandingan senilai
Dilakukan dengan perbandingan langsung antara dua keadaan atau lebih

Misalkan diketahui dua besaran A dan B

Karena berlaku perbandingan senilai maka :

Berdasarkan hubungan tersebut diperoleh :
Contoh Soal:

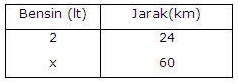
1. Sebuah kendaraan dapat menempuh jarak 24 km dengan mengkonsumsi bensin 2 liter. Berapa liter bensin yang diperlukan untuk menempuh jarak 60 km ?

Jawab :
Cara 1 :
2 liter bensin dapat menempuh jarak 24 km
1 liter bensin dapat menempuh jarak 12 km
Jadi untuk menempuh jarak 60 km diperlukan bensin sebanyak 60 : 12 = 5 liter.

Cara 2 :
Di buat tabel sebagai berikut :
Perhitungan dilakukan dengan :

Jadi untuk menempuh jarak 60 km diperlukan bensin sebanyak 60 : 12 = 5 liter.

Nah materi perbandingan senilai sudah kalian pelajari, bahkan ada 2 cara menjawab soal, silahkan dipilih alternatif mana yang kalian anggap mudah, tentunya tidak sulit bukan ?

5. Perbandingan Berbalik Nilai

Perbandingan berbalik nilai berkaitan dengan membandingkan dua buah keadaan di mana jika besaran yang satu bertambah/berkurang maka besaran yang lain berkurang/bertambah.
Masalah yang berkaitan dengan perbandingan berbalik nilai antara lain :

§  Banyaknya pekerja dengan waktu yang diperlukan untuk menyelesaikan pekerjaan (untuk pekerjaan yang sama)

§  Kecepatan dengan waktu tempuh (untuk jarak yang sama)

§  Banyaknya ternak dan waktu untuk menghabiskan makanan tersebut (untuk jumlah makanan ternak yang sama)

§  Dan sebagainya

Misalkan diketahui dua besaran A dan B
Karena berlaku perbandingan berbalik nilai maka :

Berdasarkan hubungan tersebut diperoleh :

Contoh Soal:

1. Suatu pekerjaan akan selesai dalam waktu 42 hari jika dikerjakan oleh 12 orang. Berapa lama pekerjaan yang sama akan selesai jika dikerjakan oleh 14 orang ?

Jawab :
Dibuat tabel sebagai berikut :
Perhitungan perbandingan berbalik nilai dilakukan dengan membalik Salah satu ruas:
Jadi jika pekerjaan tersebut dikerjakan oleh 14 pekerja akan selesai dalam waktu 36 hari.

Sumber : https://belajar0k3.wordpress.com/2011/04/04/perbandingan-smp-kelas-vii/